BitSet을 아시나요? (백준 2458 키 순서)
얼마전 키 순서라는 문제를 풀었습니다. 이 문제를 풀며 발견한 자바의 BitSet 클래스에 대한 이야기를 해보려고 합니다.
이 문제에 관심이 없으신 분들은 바로 비트마스킹 목차로 이동해주시면 되겠습니다.
관심이 있는 분들은 한 번 풀어보고 보시면 좋을 것 같습니다.
키 순서
문제를 간단히 설명하면 다음과 같습니다.
최대 N=500까지의 노드(학생)가 있을 때, 키 비교 결과를 가지고 각 학생의 ‘키 순서’를 정확히 알 수 있는 학생의 수를 구하는 문제.
이 문제는 플로이드 워셜로 분류되어 있으며 대부분의 블로그들은 이를 플로이드 워셜로 풀이하고 있습니다. 그러나 저는 플로이드 워셜에 익숙치 않아 DFS를 먼저 떠올렸습니다.
DFS로 각 노드에 대해 후손(자신보다 키가 작은 노드들의 집합)과 조상(자기보다 키가 큰 노드들의 집합)을 구한 뒤, 후손 노드 수 + 조상 노드 수 == N - 1이면 해당 노드의 키 순서를 확정할 수 있습니다.
각 노드는 후손 노드 수 + 조상 노드 수 == N - 1 조건을 만족하면 자신을 제외한 모든 노드가 자신보다 앞에 있는지, 혹은 뒤에 있는지 알 수 있으므로 자신의 순서를 알 수 이기 때문입니다.
이 문제는 플로이드 워셜 문제이지만 방금 설명한 것처럼 모든 노드의 후손, 조상 노드를 매번 구해서 계산해도 풀립니다.
다만 저는 노드마다 후손, 조상 노드 수를 새로 계산하는게 아니라 중복되는 계산을 메모이제이션을 통해 피해보고자 했습니다. (중복 그래프 탐색을 메모이제이션을 통해 줄이려 했습니다)

예를 들어 4번 노드의 후손 노드 수를 이미 계산했다면
6번 노드의 후손 노드 수를 새로 계산하는 것이 아닌, 4번 노드의 후손 노드의 수 + 1로 사용하는 것입니다.
하지만 단순히 이렇게 계산하면 중복 포함 문제가 발생합니다. 예를 들어 2의 후손 노드를 계산해본다고 합시다.
위에서 얘기했던 대로라면, (4의 후손 노드의 수 + 1) + (5의 후손 노드의 수 + 1)가 2의 후손 노드의 수가 될 것입니다.
그러나 이러면 5와 1이 두 번 세어지는 문제가 발생합니다.
결국 단순히 후손, 조상 노드의 수를 메모이제이션해서 풀 수는 없었습니다.
어떤 노드가 후손 노드인지도 저장해야 하는 것이죠. 이건 어떻게 구현해야 할까요?
우선 다음 방법들을 떠올려볼 수 있습니다.
1. 노드마다 boolean 배열로 후손•조상 기록하기
// 각 노드가 boolean 배열을 갖고 후손 노드를 저장합니다.
boolean[][] descendants = new boolean[n][n];
// 4, 5번 노드가 2번 노드의 후손인지 저장합니다.
descendants[2][4] = true;
descendants[2][5] = true;
// 이미 계산된 후손 노드를 활용하여 중복을 줄이려면
// 직계 후손 노드들의 boolean 배열의 합집합 연산이 필요합니다.
// 2번 노드의 후손들을 알기 위해 4번 노드와 5번 노드를 활용합니다.
for(int i=0; i<n; i++) {
descendants[2][i] = descendants[4][i] || descendants[5][i];
}길이가 N인 boolean 배열을 합쳐야 하므로 O(n)의 시간복잡도가 소요됩니다.
2. 노드마다 HashSet으로 후손•조상 기록하기
// 각 노드가 HashSet을 갖고 후손 노드를 저장합니다.
HashSet<Integer>[] descendants = new HashSet[n];
// 4, 5번 노드가 2번 노드의 후손인지 저장
descendants[2].add(4);
descendants[2].add(5);
// 이미 계산된 후손 노드를 활용하여 중복을 줄이려면
// 직계 후손 노드들의 HashSet의 합집합 연산이 필요합니다.
// 2번 노드의 후손들을 알기 위해 4번 노드와 5번 노드를 활용합니다.
descendants[2].addAll(descendants[4]);
descendants[2].addAll(descendants[5]);길이가 최대 n인 HashSet을 합쳐야 하므로 O(n)의 시간복잡도가 소요된다.
해싱 과정까지 감안한다면 조금 더 오래걸릴 수도 있다.
중복 탐색을 막기 위해 메모이제이션을 했지만, 두 방법 모두 합집합 연산으로 인해 O(n)의 시간이 소요됩니다.
이렇게 된다면 굳이 메모이제이션을 할 이유가 없습니다. 하지만 이를 타개할 방법이 있습니다. 바로 비트마스킹입니다.
비트마스킹
비트마스킹은 쉽게 설명하자면 각 비트를 boolean 배열의 원소처럼 활용하는 것입니다.
bit가 1이면 true, 0이면 false로 구분할 수 있습니다.
int 변수를 사용하면 32개의 인덱스(비트)를, long 변수를 사용하면 64개의 인덱스(비트)를 사용할 수 있습니다.
이처럼 크기가 32인 boolean 배열(약 256 비트) 대신 int변수 하나(32비트)를 사용하면서 공간을 줄일 수 있습니다.
물론 이것은 비트마스킹의 이점이지만 지금 우리에게 필요한 이유는 아닙니다.
우리에게 필요한 것은 빠른 합집합 연산입니다.
비트마스킹은 비트연산자를 활용하여 교집합, 합집합 연산 등을 O(1) 시간복잡도에 가능하게 합니다.
3. 비트마스킹으로 후손•조상 관리하기
// 각 노드마다 int 변수를 갖고 후손 노드를 저장합니다.
int[] descendants = new int[n];
// 4, 5번 노드가 2번 노드의 후손인지 저장합니다.
descendants[2] |= 1 << 4;
descendants[2] |= 1 << 5;
// 이미 계산된 후손 노드를 활용하여 중복을 줄이려면
// 직계 후손 노드들의 비트마스킹 변수의 합집합 연산이 필요합니다.
// 2번 노드의 후손들을 알기 위해 4번 노드와 5번 노드를 활용
descendants[2] = descendants[4] | descendants[5];두 int 변수를 비트 연산자 | 를 활용해 합쳐야 하므로 O(1) 시간복잡도가 소요된다.
이제 우리가 원하던 것이 가능해졌습니다. 그러나 한 가지 문제가 있습니다.
int 변수는 32개의 노드밖에 관리하지 못하는데 이 문제에서 N은 500입니다. 즉 500비트가 필요합니다.
그럼 어떻게 해야할까요?
long형 변수 8개를 사용하면 (64비트 * 8 = 512) 가능합니다.
8개 원소를 갖는 long 배열을 만들고 다음과 같이 사용합니다.
// 각 노드마다 long형 변수 8개를 갖고 후손 노드를 저장합니다.
long[][] descendants = new long[n][8];
// 배열에서 몇 번째 long인가?
int index = i / 64;
// long 내부에서 몇 번째 비트인가?
int offset = i % 64;
// 현재 노드
long[] descendant = descendants[cur];
// i번 노드가 현재 노드의 후손인지 저장합니다.
descendant[index] |= (1L << offset);위 방법을 키 순서 문제에 간단하게 대입해보면 다음과 같습니다.
long[][] descendants = new long[501][8];
// 4번 노드를 2번 노드의 후손으로 기록
int index = 4 / 64;
int offset = 4 % 64;
descendants[2][index] |= (1L << offset);
// 5번 노드를 2번 노드의 후손으로 기록
index = 5 / 64;
offset = 5 % 64;
descendants[2][index] |= (1L << offset);
// 4번 노드의 후손과 5번 노드의 후손을 2번 노드에 합친다.
for(int i=0; i<8; i++) {
descendants[2][i] = descendants[4][i] | descendants[5][i];
}
// 2번 노드의 후손 노드 개수 세기
int count = 0;
for (int i = 0; i < 8; i++) {
// bitCount: 값이 1인 비트의 개수를 세어주는 함수. 직접 구현도 가능하다.
count += Long.bitCount(descendants[2][i]);
}
System.out.println("2번 노드의 후손 수 = " + count);이제 정말 우리가 원하던 것을 해냈습니다. 하지만 꽤나 복잡합니다.
이런 복잡한 연산을 쉽게 해주는 클래스가 있습니다. 바로 BitSet입니다.
BitSet
BitSet이란 자바가 제공하는 ‘비트마스크’ 자료구조라고 할 수 있습니다.
또한 우리가 쉽게 비트마스킹을 할 수 있게 돕는 녀석입니다.
선언부는 이렇게 생겼네요.

선언부 주석에 나온 words 배열입니다. 우리가 기록할 비트들의 묶음입니다.

우리가 위에서 본 예시처럼 내부적으로 여러 long을 묶어 관리합니다.
그럼 사용법을 살펴봅시다.
// 모든 노드에 해당하는 BitSet 선언 및 초기화
BitSet[] bitSets = new BitSet[501];
for(int i=1; i<=500; i++) {
bitSets[i] = new BitSet();
}
// 4, 5번 노드가 2번 노드의 후손인지 저장합니다. (4,5 번째 비트 1로 변경)
bitSets[2].set(4);
bitSets[2].set(5);
// 2번 노드의 후손들을 알기 위해 4번 노드와 5번 노드의 비트들을 합집합한다.
bitSets[2].or(bitSets[4]);
bitSets[2].or(bitSets[5]);
// cardinality: BitSet에 1로 기록된 비트의 수를 반환
System.out.println("2번 노드의 후손 개수: " + bs.cardinality());이외에도 비트를 0으로 변경하는 clear, 교집합 연산을 하는 and 등 다양한 연산자를 제공합니다.
이것은 위에서 본 예시와 조금 다른 set 함수입니다.
원래 1을 기록할 땐 set, 0을 기록할 땐 clear지만
boolean 매개변수를 활용해 아래 set 함수 하나만 이용해도 되도록 합니다.

범위로 여러 비트의 값을 지정할 수도 있습니다.
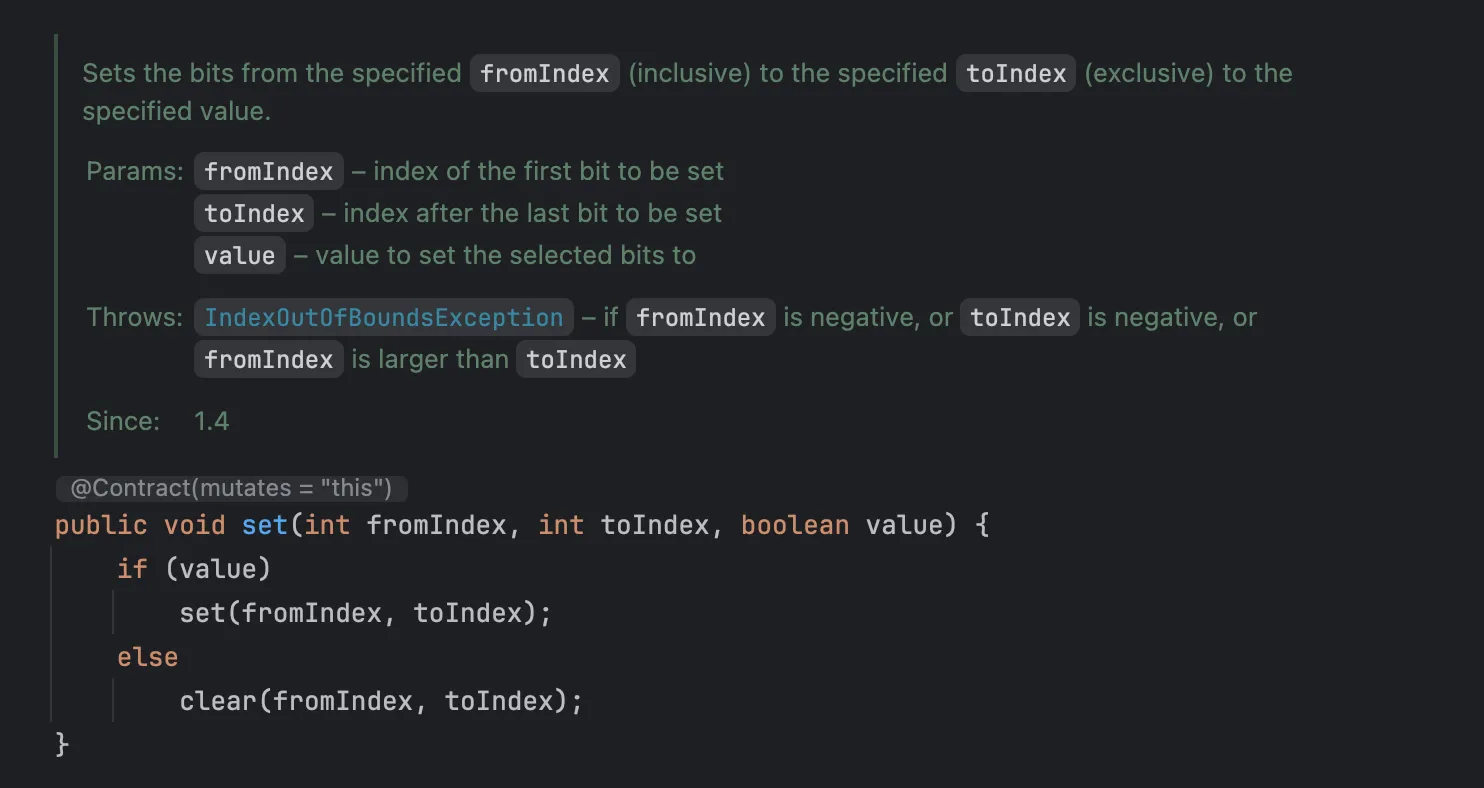
다음처럼 특정 비트의 값을 boolean으로 가져올 수도 있습니다.
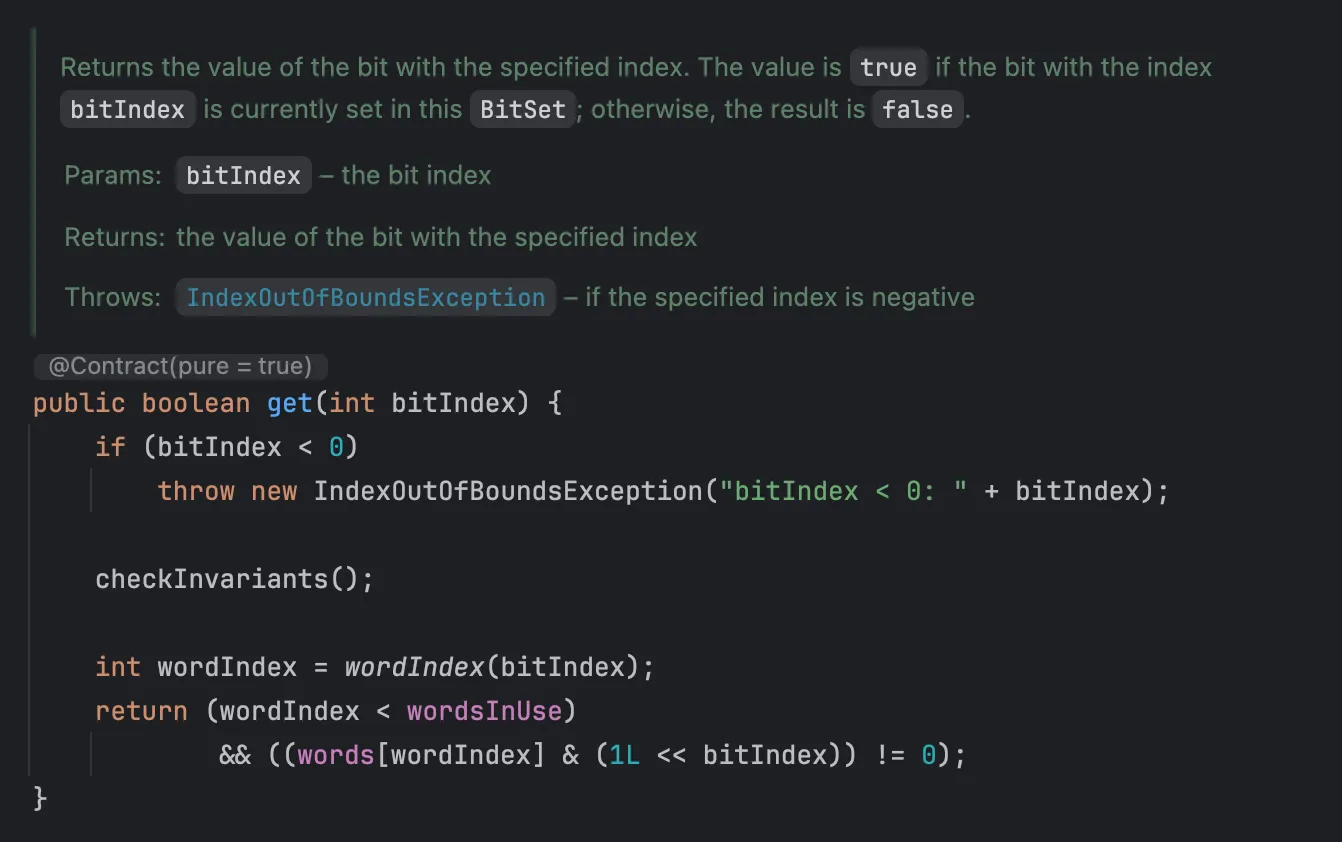
값이 1인 비트의 수를 반환하는 cardinality() 함수는 다음과 같습니다.
우리가 사용했던 Long.bitCount를 그대로 사용하는 것을 볼 수 있습니다.

이렇게 BitSet을 이용하면 비트마스킹을 편하게 구현할 수 있습니다.
물론 비트마스킹의 원리를 모르고 사용하면 안되겠죠?
마무리
원래 알고리즘 문제 풀이 관련 글은 블로그에 올리지 않는 것이 제 규칙이었으나
이번에 BitSet을 발견하고 그 편리함에 놀라 공유하고자 이번 주제로 선정하게 됐습니다.
추가로 키 순서 문제를 여러 방법을 푼 실행 시간을 보면 다음과 같습니다.
- DFS로 매번 탐색 → 약 1700ms
- DFS + HashSet → 약 1600ms
- 플로이드 워셜 → 약 830ms
- DFS + 비트마스킹(BitSet) → 약 390ms
확연한 시간 차이를 볼 수 있습니다.
앞으로 여러분의 비트마스킹 문제 풀이 시간 단축에 도움이 되길 바라며 글을 마치겠습니다.